充满机遇的物理层
探索计算机网络OSI模型中的物理层的故事.
现在我们来到了计算机网络的OSI模型的第一层:物理层(physical layer)。在这里我会以教授的slides为框架简要的讨论物理层中发生的故事,主要会关注从数字信号与模拟信号之间的转化过程,这是属于离散和连续的较量呢。之所以说是充满机遇的是因为离散与连续之间有着隐藏法术等待我们去习得。
信号和信息
要想理解物理层中发生的种种有意思的事情(当然主要是数学故事啦),还是得要有些准备工作要做的。 我们不妨看看物理层到底干了些什么:
物理层利用传输介质为通信的两端建立、管理和释放物理链接,实现比特流的透明传输,保证比特流正确的传输到对端。物理层中承载的是比特流单位是比特(bit)。我知道我已经说的这么清楚明白,你可能依然犹如漫步在云端,头重脚轻不明所以。那么我用一个生活中的例子来帮助你更好的理解。
例:比如你在和朋友聊天,说话内容需要由大脑编排好,然后将你要讲的内容送达到嘴巴,嘴巴通过发出声音让对方听到你说话的内容。并且你在讲话时也无需考虑声波会如何传送到对方的耳朵中的,并且你也看不到声波是如何传达到对方的耳朵中的。这里声波就可以理解为是‘比特流’,你的嘴巴就是提供了‘物理层’的服务。
嘴巴负责开始谈话(建立链接)、判断谈话的开始和结束(管理链接)、结束谈话(释放链接)。并且嘴巴也无需考虑声波是如何传达到对方的耳朵中,所以声波对于嘴巴是透明的。在网络中‘透明’=管理成本低。
我们知道通过信号的强弱变化可以传递出二进制编码,而这些编码被识别成不同的符号,通过这些符号也就可以传达出各种各样的信息。 在信息论中我们其实可以通过引入物理学中熵(entropy)的概念来量化信息,接收到消息中包含的信息量又称作信息熵。事实上,1948年Shannon就是这么做的,将热力学的熵引入信息学中, 于是我们可以这样来定义信息:
信息,一方面可以理解为能够预测信号变化的不确定性。于是一个字母表X中的x的信息内容取决于信息携带信号在观察时该x的出现概率,于是定义为: $$ I(x)=-\log_{2}{p(x)} $$ 单位为bit。
信息熵于是可以由求期望的方式给出: $$ H(X)=\sum_{x\in X} p(x)I(x) = - \sum_{x\in X}p(x)\log_{2}{p(x)} $$
信号处理(Signaldarstellung)
在物理层传输介质中传输的信号共分为两种,模拟信号、数字信号,下图给出了这两种信号的范例:
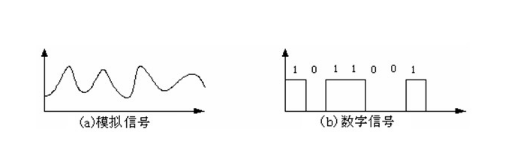
模拟限号和数字信号
由于计算机只能识别数字信号,但要在广域网中传播却又以模拟信号的形式进行(光纤的情况又有不同,这个就是后话了),于是我们会设置一个调制解调器把数字信号转化为模拟信号以及反向的过程。 而接下来我们就来讨论这两过程的细节问题。
数学基础
开头就有说物理层的故事是属于离散和连续之间的较量,虽说离散和连续这两个相对的概念之间是只有较量,但是使用合适的方法这二者却又可以互相转换,这也就是我们要在这部分说明的神奇的数学法术。
当然如果你有足够的悟性就又可以领悟到这两个史诗级别的法术呢。
傅里叶级数(Fourier series)
在数学中,傅里叶级数能把任何周期函数或周期信号分解成一个(可能由无穷个元素组成的)简单振荡函数的集合,也即正弦和余弦函数,同时也是我们后面会说到的采样定理的核心内容。
我这里直接给出教授slides上面的定义:
Ein periodisches Signal s(t) lässt sich als Summe gewichteter Sinus- und Kosinus-Schwingungen darstellen. Die so entstehende Reihenentwicklung von s(t) bezeichnet man als Fourierreihe:
$$ s(t)=\frac{a_0}{2} + \sum_{k=1}^{\infty} {a_k\cos{k{\omega}t} + b_k\sin{k{\omega}t}} $$
这里的$a_0$是相对y轴的偏移量,同时$a_k$和$b_k$这两个系数可以由如下定义:
$$ a_k = \frac{2}{T}\int_0^T {s(t)\cos{k{\omega}t}} {\rm d}t $$
$$ b_k = \frac{2}{T}\int_0^T {s(t)\sin{k{\omega}t}} {\rm d}t $$
傅里叶变换(Fourier transform)
傅里叶变换是一种线性积分变换,用于信号在时空域和频域之间的变换。实际上借用维基百科的话来说傅里叶变换就像化学分析,确定物质的基本成分;信号来自自然界,也可以对其进行分析,确定其基本成分。
Die Fourier-Transformierte einer stetigen, integrierbaren Funktion s(t) ist gegeben als $$ s(t) \longrightarrow S(f) = \frac{1}{\sqrt{2\pi}}\int_{t=-\infty}^{\infty} {s(t)(\cos{2\pi ft}-i\sin{2\pi ft})} {\rm d}t $$ 其中$i=\sqrt{-1}$ , 当然这里也可以写成指数形式,就不再赘述。
采样,重构和量化
有了前文的数学基础后,我们就可以开始学习信号处理过程中的采样(sampling, Abtastung),重构(Rekonstruktion),以及量化(Quantisierung),从而达到让人激动的离散与连续之间的转化。更具体来说,采样(时域离散)和量化(值域离散)相结合可将模拟信号转换为数字信号,重构则可以认为是采样的逆过程。其中著名的"Nyquist-Shannon sampling theorem", 也即“奈奎斯特–香农采样定理”,的内容是连续信号与离散信号之间的一个基本桥梁,其实更像是对于转换的限制条件,这里在后面会更详细聊到。
采样(Abtastung)
我们这里先看看维基百科上是怎么说的:
在信号处理领域,采样是将信号从连续时间域上的模拟信号转换到离散时间域上的离散信号的过程,以采样器实现。通常采样与量化联合进行,模拟信号先由采样器按照一定时间间隔采样获得时间上离散的信号,再经模数转换器(ADC)在数值上也进行离散化,从而得到数值和时间上都离散的数字信号。
通过采样得到的信号,是连续信号(例如,现实生活中的表示压力或速度的信号)的离散形式。连续信号通常每隔一定的时间间隔被模数转换器(ADC)采样,当时时间点上的连续信号的值被表现为离散的,或量化的值。
这样得到的信号的离散形式常常给数据带来一些误差。误差主要来自于两个方面,与连续模拟信号频谱有关的采样频率,以及量化时所用的字长。采样频率指的是对连续信号采样的频度。它代表了离散信号在和时域和空间域上的精确度。字长(比特的数量)用来表示离散信号的值,它体现了信号的大小的精确性。
再来看看教授的slide上面怎么说的:
Das Signal s(t) wird mittels des Einheitsimpulses (Dirac-Impulses) $\sigma[t]$ in äquidistanten Abständen $T_a$ (Abtastintervall) für n $\in$ Z abgetastet:
$$
\hat{x}=s(t) \sum_{n=-\infty}^{\infty}\sigma[t-nT_a]=
\begin{cases}
1, & t=nT_a \newline
0, & sonst\
\end{cases}
$$
Da $\hat{s}(t)$ nur zu den Zeitpunkten nTa für ganzzahlige n von Null verschieden ist, vereinbaren wir die Schreibweise $\hat{s}[n]$ für zeitdiskrete aber wertkontinuierliche Signale.
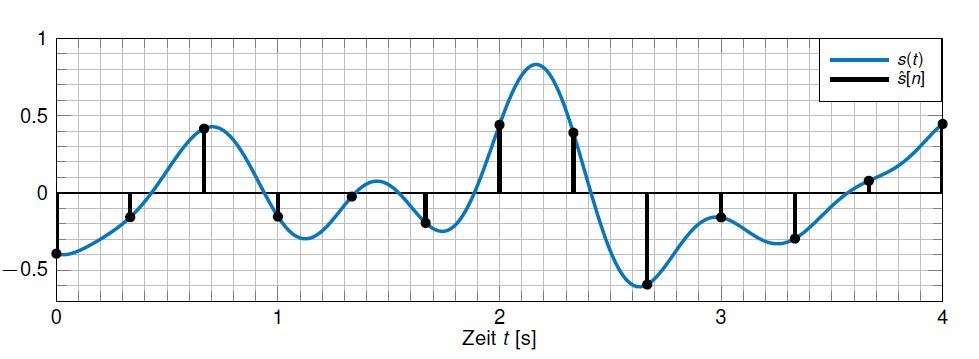
Zeitkontinuierliches Signal und Abtastwerte
重构
在这个过程中数字信号被转换成模拟信号,就如同把采样的过程逆转一样,称作demodulation。在理想的系统上,每经过取样的固定时间而读取新的数据时,输出会即时改变到该强度。经过这样的即时转换,离散的信号本质上会有大量的高频率能量,出现与采样率的倍数相关的谐波。要消灭这些谐波并使信号流畅,信号必须通过一些模拟滤波器,压制任何在预期频域外的能量。
时域中的乘法对应于频域中的卷积: $$ s(t) \delta [t -nT] \rightarrow \frac{1}{T}S(f)*\delta[f - n/T] $$

Reconstruction
香农定理
香农定理给出了信道通信传送速率的上限和信噪比以及带宽的关系。
Abtasttheorem von Shannon und Nyquist Ein auf |f | $\leq$ B bandbegrenztes Signal s(t) ist >vollständig durch äquidistante Abtastwerte ˆ s[n] beschrieben, sofern diese nicht weiter als $T_a \leq$1/2B auseinander liegen. Die Abtastfrequenz, welche eine vollständige Signalrekonstruktion >erlaubt, ist folglich durch:
$$ f_a \geq 2B $$ nach unten beschränkt.
量化
传输信道
对于无噪声,M的通道,我们会有$M = 2^N$种可区分的符号,可实现的数据率如何变化呢?
我们先来回顾一下熵: 假设信号源以相同的概率发射所有信号,这样信号源的熵(因而平均信息)最大。
对于宽度为B的信道上的传输速率,我们可以得到最大传输速率:
Harleys Gesetz $C_H = 2B \log_{2}(M) bit$
同时还有新的定义:信号功率(Signallesitung) 信号振幅的平方的期望值与信号功率的平方相对应。方差(分散)信号的振幅对应于不含直流分量的信号功率,并代表信息承载量信号的功率。
回到正题,不妨想想在有