从有穷自动机到正则语言
在上篇中我们了解到DFA与NFA的故事,从中我们初识了正则运算并且了解到其封闭性(虽然我还没有写完),在本篇中我们将会里了解到正则表达式,进而到正则语言,我们可以从这个小小的角度对归纳的魅力有惊鸿一瞥,还可以了解到有穷自动机,正则表达式,正则语言它们之间的转换。
正则表达式及形式化定义
正则表达式其实是正则语言(formal language)的另一种定义。
我们不妨来看看定义,这里其实就可以就感受到归纳的威力了! R是正则表达式(RE)当且仅当R是
- a, $a \in \Sigma$; /表示 {a}/
- $\epsilon$ /表示 ${\epsilon}$/
- $\emptyset$
- $(R_1 \cup R_2),R_1和 R_2都是正则表达式;$
- $(R_1 R_2), R_1和R_2都是正则表达式;$
- $(R_1^ *),R_1是正则表达式.$
L(R): R表示的语言
正则语言封闭性
有空再写吧,本质还是构造法
正则表达式与有穷自动机的等价性
我们已经知道有穷自动机识别的语言是正则语言,而后我们又认识到正则表达式(regular expression,RE)也可以来定义语言,他们两者的关系是怎样的呢?下面我们就来证明正则表达和有穷自动机是等价的。
等价,参考上一篇文章也就是说他们能够描述同样的语言。
我们要证明的也就是以下定理:
Satz 3.19 (Kleene 1956) Eine Sprache L $\in$ $\Sigma^{*}$ ist genau dann durch einen regulären Ausdruck darstellbar, wenn sie regulär ist.
这也其实就是要我们证明:一个语言是正则的当且仅当可用正则表达式描述这个语言。
我们要做的其实也就是有一个正则表达式,我们要构造一个有穷自动机识别正则表达式产生的那些串;然后给定一个自动机,我们要构造一个正则表达式使得这个RE描述的串正好是自动机识别的串,所以我们要给定一个算法能在有穷自动机和相应的RE之间进行转换,并且这种转换是等价的。
先来看看 “$\implies$” 方向: 这里需要做的其实是就是构造一个有穷自动机去识别相应的语言,也就是将一个正则表达式转换为自动机。关于自动机其实为了方便只需要关注NFA就可以了,因为上一篇文章中我们已经证明了DFA和NFA的等价性。 正则表达式是通过前文说的6个基本步骤来定义的,前三个是基本步骤,后三个是归纳步骤;我们只需说明对于每一个步骤如何去构造相应的有穷自动机即可完成证明。
-
R = a, a$\in\Sigma$. L(R) = {a}, N = ({$q_1$, $q_2$ }, $\Sigma$, $\delta$, $q_1$, {$q_2$} ), $\delta (q_1, a)$ = ${q_2 }$, $\delta (r, b) = \emptyset$, 若$r\neq q_1$或$b \neq a$ (其实就是只有a的语言)
-
R = $\epsilon$. L(R) = {$\epsilon$}, N = ( {$ q_1 $}, $\Sigma, \delta, q_1$, {$q_1$} ), $\forall r, \forall b, \delta (r, b) = \emptyset$. (只有一个状态$q_1$接受空串,其他串都不接受)
-
R = $\emptyset$. L(R) = $\emptyset$, N = ( {$q_1 $}, $\Sigma , \delta , q_1, \emptyset$), $\forall r, \forall b, \delta(r,b)=\emptyset$. (只有一个状态$q_1$,但区别不是接受状态,也即什么串也不接受)
-
$R=(R_1 \cup R_2)$, 这里直接上教授slides上面的图
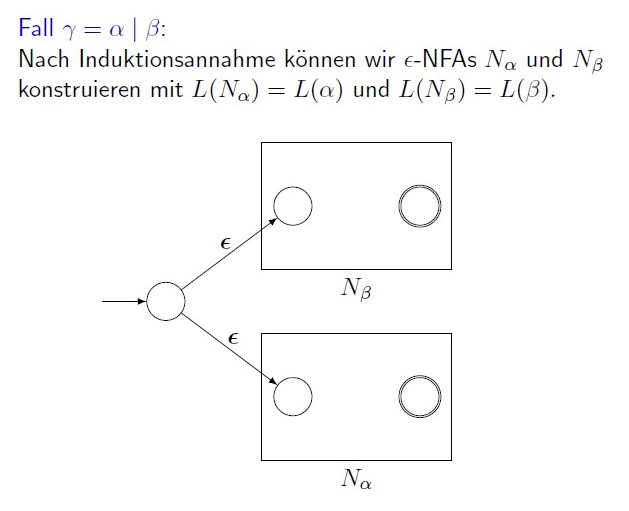
并/alternative
这个新自动机的接受状态为原来接收状态的并,并且用一个新的初始状态来代替旧的。
-
$R=(R_1 R_2)$, 这里还是看图说话
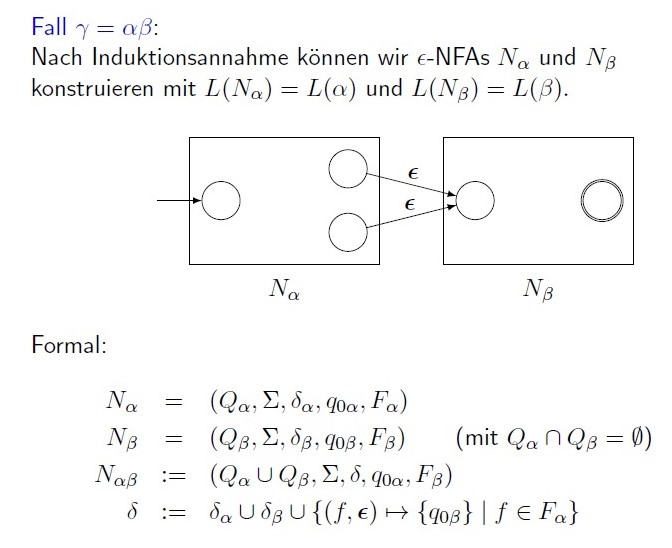
连接/concatenation
这个新自动机接受状态为后一个的接受状态,而初始状态只有第一个的了。
-
$ R =(R_1 ^*)$, 还是直接给出图比较直观
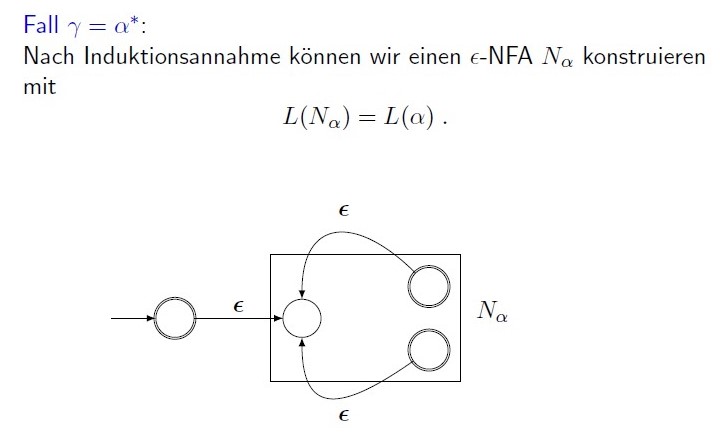
星号/star
加入一个新的初始状态,并且本身是一个接收状态,这样可以保证接受$\epsilon$空串,然后通过$\epsilon$连接新旧初始状态,和接受状态。
这一个方向证毕。
再来看看 “$\Longleftarrow$” 方向: 这里其实有两种证明方式,一种是通过定于广义非确定型有穷自动机来证明,还有一种是Tobia教授课上给出的一种算法,我们不妨都来学习学习。
先来看看Tobias教授给出的算法:
Sei $M = (Q, \Sigma ,\delta , q_1 , F) ein DFA$. (Funktioniret analog auch für NFA) WIr konstruieren einen RE $\gamma$ mit L(M) = L ($\gamma $).
Sei Q = {$q_1 ,…,q_n$}.Wir setzen
$$ R_{ij}^{k}:= \lbrace w \in \Sigma ^* | die \ Eingabe\ w \ führt\ von\ q_i\ in\ q_j ,wobei\ alle
Zwischenzustände (ohne\ ersten\ und\ letzten) einen\ Index\ \leq k\ haben\ \rbrace $$Behauptung:
Für alle $i, j \in \lbrace1,…,n\rbrace und\ k \in \lbrace 0,…,n \rbrace können\ wir\ einen\ RE\ L(\alpha {ij}^k) = R{ij}^k$
Induktion über k: k = 0: Hier gilt
再来看看另一种证法: 其实也就是定义一个广义非确定型有穷自动机(GNFA),从DFA构造等价的GFNA,从GFNA构造等价的正则表达式。
GFNA的特殊在于状态间的转移不
泵引理
泵引理(Pumping Lemma für reguläre Sprachen),用来证明一个语言不是正则的神奇工具。有些语言看起来很规则,但是却不是正则语言,因为无法用有穷自动机来描述,我们用泵引理即可很有效地判断不是正则语言的情况,但却无法证明是正则语言,因为只是必要条件而不是充分条件。下面来看看泵引理具体长什么样子,既有中文版,也有德语版:
泵引理:设A是正则语言,则存在常数p(称为泵长度),使得若 s $\in$ A且 |s| $\geq$,则 s = xyz,并且满足下述条件:
- $\forall i \geq 0, xy^iz \in A;$
- |y| > 0;
- |xy| $\leq p$.
这里第一个条件其实很有意思,这其实很像前面广义非确定有穷自动消除一个顶点后出来的表达式,实际上并不是巧合,从某个状态出发读了x之后进入一个状态,这个状态自己到自己有一个箭头,并且可以通过 y 来到达,这个状态读取 z后到接受状态(这个样子其实和水泵也很像)。
接下来看看德语版:
Satz 3.30 (Pumping Lemma für reguläre Sprachen) Sei R $\subseteq \Sigma ^*$ regulär. Dann gibt es ein n > 0, so dass sich jedes z $\in$ R mit |z| $\geq$ n so in $z = uvw$ zerlegen lässt, dass
$v \neq \epsilon$ $|uv| \leq n$, und $\forall i \geq 0. uv^iw \in R$.
泵引理来证明语言不是正则的其实就是要来用上面的条件来推矛盾,有时候就需要灵感来取一个特殊的s,经过泵的步骤后就不在这个语言中了,就有了矛盾。
泵引理的证明
在这个证明中我们会明白如何取这个常数 p,为什么s会被分为三段,为什么xy的长度要小于等于p。 提前剧透:这里的p其实就是一个相应自动机的状态数。
证明:设A = L(M), M = (Q, $\Sigma ,\delta ,q_1, F$), |Q| = p, $s = s_1s_2…s_n \in A, n \geq p$. 设M在s上计算 $r_1,r_2,…,r_{n+1}, \delta({r_i, s_i}) = r_{i+1}$
$r_i$为n+1个状态,经由s的n个输入字符可到达。由于总共只有p个状态,并且不超过n,而现在有n+1个状态,每一个都是Q中的元素,由著名的抽屉原理:这n+1个状态中最多只有p种不同的状态, 也就是说至少会有两个重复的状态。
根据抽屉原理,存在 j < l, 使得 $r_j = r_l , l \leq p + 1$. 令 $x = s_1 …s_{j - 1}, y=s_j …s_{l - 1}, z=s_l …s_{n+1}$. 由于$x让M从r_1 到r_j,y让M从r_j到 r_j, z让M从r_j到r_{n+1}, 而r_{n+1}是接受状态,所以\forall i \geq 0, xy^iz \in A.$
由于$j \neq l , 所以|y|>0$. 由于$l \leq p+1, 所以|xy| \leq p$.
这样就完成了泵引理的证明。
Tobia教授slides上面的证明也很类似:
Sei R = L(A), A = ($Q, \Sigma , \delta , q_0 , F$). Sei n = |Q|. Sei nun z = $a_1a_2a_3…a_m \in R$ mit m $\geq n$. Die beim Lesen von $z$ durchlaufene Zustandfolge sei $q_0 = p_0 \rightarrow ^{a_1} p_1 \rightarrow ^{a_2}p_2 … \rightarrow ^{a_m} p_m$ Dann muss es $0 \leq i \leq j \leq n geben mit p_i = p_j$. Wir teilen $z$ wie folg auf:
$$ \underbrace{a_1…a_i}u\underbrace{a{i+1}…a_j}v \underbrace{a{j+1}…a_m}_w $$
Damit gilt: $|uv| \leq n$ $v \neq \epsilon$, und $\forall l \geq 0 . uv^l w \in R$
Ardens Lemma
Ardens Lemma, 也叫 Arden’s rule, 用来构造这样的自动机:只有一个初始状态,且其中没有$\epsilon$移动。先来看看数学表达式长什么样,再来翻译翻译到底说了些啥。 $$ \text{Sind A, B und X Sprachen mit} \epsilon \notin \text{A, so gilt }\ X = AX \cup B \Rightarrow X = A^B \ \text{其中还有一个类似的推论:} Sind\ \alpha , \beta \text{ und X regulär Ausdrücke mit } \epsilon \notin L(\alpha), so\ gilt \ X \equiv \alpha X | \beta \Rightarrow X \equiv \alpha ^ \beta $$
于是有了这些的结论: